今まで因子分析について扱ってきた。次として、だいぶジャンプかもしれないが構造方程式モデリングを触ってみようと思う。今回はとりあえず動きそうな例を考えてみて、そのデータに対してPythonの semopy で構造方程式モデリングを動かすところまでを試してみようと思う。
はじめに
たまたま、自分がよく読むタイプのものが、データを元にその背景にあるメカニズムを説明するのに、構造方程式モデリングをよく利用している。前から気になっていたこともあり、触りながら理解してみようと思って、今回に至った。
SEM: Structural Equation Modeling とも呼ばれる構造方程式モデリングだが、共分散構造分析というタイトルで日本語のWikipediaはページが作られている。一方で英語側は Structural Equation Modeling のページがある。細かい部分はまだよく理解していないが、構造方程式モデリングには共分散をベースにしたものと、部分最小二乗法(PLS: Partial Least Squares)を利用したものがあるだということはよく出てくる。(よく出てくると言っておいて、出てきた参考文献は忘れた笑)
今回の範囲としては、あまりスコープは広げずに、Pythonの semopy で動く範囲を考えようと思う。おそらく共分散をベースにしたSEMのはず。
環境
Pythonは 3.12.11 で動作させた。
途中、PythonコードないでGraphvizを利用して、ネットワークグラフを書いた。Graphvizのバージョンは 14.0.2 。
例
例として、居心地の良いカフェを考える。アンケート結果として、コーヒーの味、店のデザイン、混雑度、居心地の良さ、が5段階のリッカード尺度であるとする。潜在変数として、店主のセンス、があるとして、構造方程式モデリングをしてみようと思う。
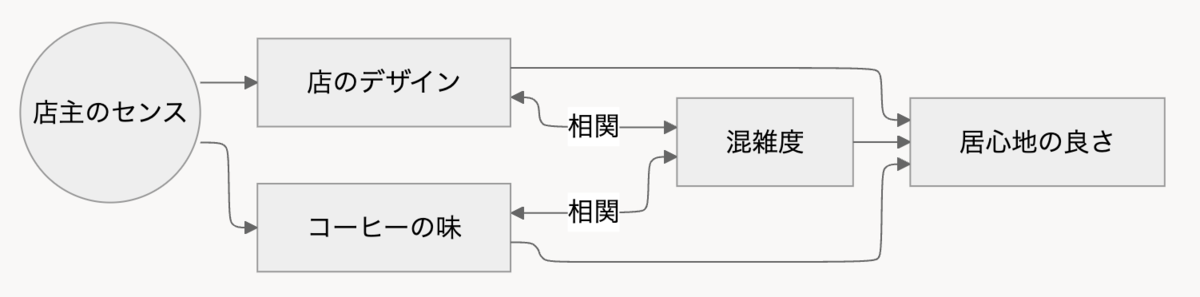
例えば、こんな構造をイメージして、ダミーデータを作ってもらおうと思う。今回は最近使ってみているChatGPTに作ってもらおうと思う。
構造方程式モデリングを行うためのダミーデータを作成してください。 背後にある観測変数や潜在変数の構造は以下とします。 ```mermaid flowchart LR id1(("店主のセンス")) --> id2["店のデザイン"] <-->|相関| id3["混雑度"] --> id4["居心地の良さ"] id2 --> id4 id1 --> id5["コーヒーの味"] --> id4 id5 <-->|相関| id3 ``` 以下の観測変数について、5段階のリッカード尺度で回答されるとし、ダミーデータを作成してください。 - 店のデザイン - 混雑度 - 居心地の良さ - コーヒーの味 サンプルサイズ = 300とし、300件のデータを作成してください。 出力するデータは300件の表形式とし、CSVによるコードブロックで出力してください。
上のプロンプトを入れてみるとデータを作成してくれた。作成されたデータはGitHubに置いておく。
semopy を試してみる
本来予想すべき構造からデータを作ってしまい、現状答えがわかっている状況ではあるのだが、構造を考えて semopy に入れてみようと思う。
import pandas as pd from sklearn.preprocessing import StandardScaler import semopy from semopy import Model, semplot # Step 1: データの準備 # データセット読み取り df = pd.read_csv("../data/sem_dummy_data.csv") # データの標準化 scaler = StandardScaler() scaled_data = scaler.fit_transform(df) scaled_df = pd.DataFrame(scaled_data, columns=df.columns) # Step 2: モデル構造の定義 # 店主のセンス → 店のデザイン, コーヒーの味 # 店のデザイン, コーヒーの味, 混雑度 → 居心地の良さ # 店のデザイン ↔ 混雑度 # コーヒーの味 ↔ 混雑度 model_desc = """ # 潜在変数の定義 店主のセンス =~ 店のデザイン + コーヒーの味 # 構造モデル 居心地の良さ ~ 店のデザイン + コーヒーの味 + 混雑度 # 相関関係 店のデザイン ~~ 混雑度 コーヒーの味 ~~ 混雑度 """ # Step 3: モデルの作成とフィッティング model = Model(model_desc) model.fit(df) # Step 4: 結果の出力 # 推定されたパス係数など estimates = model.inspect() print("=== 推定結果 ===") print(estimates) # 適合度指標 print("\n=== 適合度指標 ===") print(semopy.calc_stats(model).T) # Step 5: モデルの可視化 # PNGとして保存 semopy.semplot(model, "01_sem01.png", plot_covs=True, engine="dot")
以上のコードから、数値も出てきて、かつどれぐらいモデルが適合しているか、という数値が出る。コードのかなりの部分は各種ChatGPTなり、Github Copilotが作ってくれたところが多いが…
=== 推定結果 ===
lval op rval Estimate Std. Err z-value p-value
0 店のデザイン ~ 店主のセンス 1.000000 - - -
1 コーヒーの味 ~ 店主のセンス 0.545532 4618447.495721 0.0 1.0
2 居心地の良さ ~ 店のデザイン 0.222457 0.050418 4.412274 0.00001
3 居心地の良さ ~ コーヒーの味 0.293362 0.049174 5.965794 0.0
4 居心地の良さ ~ 混雑度 -0.316084 0.045914 -6.88431 0.0
5 店のデザイン ~~ 混雑度 0.186010 0.034469 5.396421 0.0
6 店のデザイン ~~ 店のデザイン 0.245257 2965820.800758 0.0 1.0
7 コーヒーの味 ~~ 混雑度 0.090139 0.035341 2.550533 0.010756
8 コーヒーの味 ~~ コーヒーの味 0.478809 882644.016181 0.000001 1.0
9 店主のセンス ~~ 店主のセンス 0.350323 2965820.800758 0.0 1.0
10 居心地の良さ ~~ 居心地の良さ 0.377361 0.030811 12.247449 0.0
=== 適合度指標 ===
Value
DoF 0.000000e+00
DoF Baseline 7.000000e+00
chi2 2.497968e-06
chi2 p-value NaN
chi2 Baseline 1.492459e+02
CFI 1.000000e+00
GFI 1.000000e+00
AGFI NaN
NFI 1.000000e+00
TLI NaN
RMSEA inf
AIC 2.000000e+01
BIC 5.703782e+01
LogLik 8.326561e-09
出力が以上の通りなのだが、 CFI や GFI などが重要な値らしい。が、自分の初心感が爆裂しており、この結果は使えないらしい笑
というのが、たとえば chi2 p-value や AGFI という値が NaN となってしまっている。これは構造の自由度が0となっており、予想した構造にパスが多すぎて、全ての変数を説明できる形になってしまっているようだ。
試しに
# Step 2: モデル構造の定義 # 店主のセンス → 店のデザイン, コーヒーの味 # 店のデザイン, コーヒーの味, 混雑度 → 居心地の良さ # 店のデザイン ↔ 混雑度 # コーヒーの味 ↔ 混雑度 model_desc = """ # 潜在変数の定義 店主のセンス =~ 店のデザイン + コーヒーの味 # 構造モデル 居心地の良さ ~ 店のデザイン + コーヒーの味 + 混雑度 # 相関関係 店のデザイン ~~ 混雑度 コーヒーの味 ~~ 混雑度 """
のうちの、相関関係の箇所をいくつかコメントアウトしてみた。そうしたところ各種数値が NaN とならずに出力された。いくつか試してみたが、結論としては以下の構造が良さそうだ。
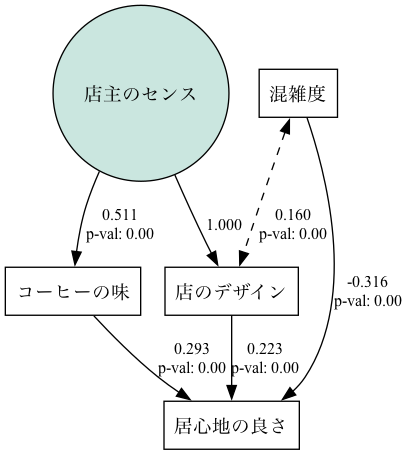
ChatGPTに作ってもらったダミーデータではあるが、このデータにとっては「コーヒーの味」よりも「店のデザイン」の方が混雑度に関係があると考えているデータのようだ。まあ、世の中のカフェを考えた時、必ずしも味や店の雰囲気と混雑の間に相関が大きいわけでもないだろうし、混雑は立地なども普通影響すると思う。ダミーデータとはいえ、ChatGPTが空気を読んでそう作ってくれたのかもしれない。
まとめ
まずはこれぐらいの短めで。正直これだけでも、まずは動かす部分でまあまあ苦労した気がする笑
あまり直接的ではないが、久しぶりにGraphvizを使ったが、まあちゃんと書いてくれるものだな笑 10年以上前の学生の頃からずっと使われているツールであることがすごいと思う。
SEMに戻ると、動かしてはみたものの、まだまだ勉強すべき点が多いと感じた。体系的に学ぶべきなのかもしれないが、まあ趣味ではあるし、ある程度手を動かしつつ各種適合度の数値などを理解していき、確認的因子分析全般の理解にも繋げていきたいと思う。
参考資料
- Wikipedia共分散構造分析
- WikipediaStructural equation modeling
- Georgy Meshcheryakovsemopy: Structural Equation Modeling in Python: 今回利用したSEMのPythonライブラリ。上記のWikipediaにも紹介がある。
- Qiita【実践】構造方程式モデリング - Qiita: Graphvizで描画するコードは参考にさせていただいた。
- AIcia Solid Project【潜在変数の関係を探る】構造方程式モデリング - 実応用の豊富な基礎分析なのです【いろんな分析 vol. 6 】 #06…: ざっくりの考え方を参考にした。